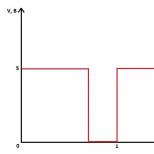
التمثيل الهندسي للأعداد العقلانية. مجموعة الأعداد الحقيقية. العمليات على المجموعات تمثيل مجموعات الأرقام على خط الإحداثيات
الفصل الأول. المتغيرات والوظائف§1.1. أرقام حقيقية
يتم التعرف الأول على الأعداد الحقيقية في دورة الرياضيات المدرسية. يتم تمثيل كل عدد حقيقي بكسر عشري محدود أو لا نهائي.
تنقسم الأعداد الحقيقية إلى فئتين: فئة الأعداد النسبية وفئة الأعداد غير المنطقية. عاقِلهي الأرقام التي لها النموذج، أين مو نهي الأعداد الصحيحة coprime، ولكن 
. (يتم الإشارة إلى مجموعة الأرقام العقلانية بالحرف س). يتم استدعاء الأرقام الحقيقية المتبقية غير منطقي. أرقام نسبيةيتم تمثيلها بكسر دوري محدود أو لا نهائي (مثل الكسور العادية)، فإن تلك الأعداد الحقيقية التي يمكن تمثيلها بكسور غير دورية لانهائية ستكون غير منطقية.
على سبيل المثال، الرقم 
- عقلاني، و 
, 
, 
وما إلى ذلك وهلم جرا. - أرقام غير منطقية.
يمكن أيضًا تقسيم الأعداد الحقيقية إلى أعداد جبرية - جذور كثيرة الحدود ذات معاملات عقلانية (تشمل هذه، على وجه الخصوص، جميع الأعداد النسبية - جذور المعادلة 
) – وإلى المتعالي – كل الباقي (على سبيل المثال، الأرقام 
و اخرين).
يتم الإشارة إلى مجموعات جميع الأعداد الطبيعية والأعداد الصحيحة والحقيقية وفقًا لذلك على النحو التالي: نز, ر
(الأحرف الأولى من الكلمات Naturel، Zahl، ReReel).
§1.2. صورة الأعداد الحقيقية على خط الأعداد. فترات
هندسيًا (من أجل الوضوح)، يتم تمثيل الأعداد الحقيقية بنقاط على خط مستقيم لا نهائي (في كلا الاتجاهين) يسمى عددي
محور. ولهذا الغرض، يتم أخذ نقطة على الخط قيد النظر (الأصل هو النقطة 0)، ويشار إلى الاتجاه الإيجابي، ويصور بواسطة سهم (عادةً إلى اليمين) ويتم تحديد وحدة مقياس، والتي يتم وضعها جانباً إلى أجل غير مسمى على جانبي النقطة 0. هكذا يتم تصوير الأعداد الصحيحة. لتمثيل رقم بمنزلة عشرية واحدة، تحتاج إلى تقسيم كل قطعة إلى عشرة أجزاء، وما إلى ذلك. وبالتالي، يتم تمثيل كل عدد حقيقي بنقطة على خط الأعداد. العودة إلى كل نقطة 
يتوافق مع عدد حقيقي يساوي طول القطعة 
ويتم التقاطها بعلامة "+" أو "-"، اعتمادًا على ما إذا كانت النقطة تقع على يمين نقطة الأصل أو على يسارها. بهذه الطريقة، يتم إنشاء تطابق واحد لواحد بين مجموعة جميع الأعداد الحقيقية ومجموعة جميع النقاط على محور الأعداد. يتم استخدام المصطلحين "الرقم الحقيقي" و"نقطة محور الرقم". المرادفات.
رمز 
سنشير إلى كل من الرقم الحقيقي والنقطة المقابلة له. الأرقام الموجبة تقع على يمين النقطة 0، والأرقام السالبة تقع على اليسار. لو 
، ثم على محور الرقم النقطة 
تقع على يسار النقطة 
. دع هذه النقطة 
يتوافق مع الرقم، ثم يسمى الرقم إحداثيات النقطة، والكتابة 
; في كثير من الأحيان يتم الإشارة إلى النقطة نفسها بنفس الحرف مثل الرقم. النقطة 0 هي أصل الإحداثيات. يتم تحديد المحور أيضًا بالحرف 
(الشكل 1.1).
أرز. 1.1. محور الرقم.
مجموعة جميع الأرقام الكذب بينأرقام معينة ويسمى الفاصل الزمني أو الفجوة؛ قد تكون الغايات ملكًا له وقد لا تكون كذلك. دعونا نوضح هذا. يترك 
. مجموعة من الأرقام التي تحقق الشرط 
، ويسمى الفاصل الزمني (في بالمعنى الضيق) أو الفاصل الزمني المفتوح، المشار إليه بالرمز 
(الشكل 1.2).
أرز. 1.2. فاصلة
مجموعة من الأرقام مثل ذلك 
يسمى الفاصل الزمني المغلق (مقطع، مقطع) ويشار إليه بـ 
; على محور الرقم تم وضع علامة عليه على النحو التالي:
أرز. 1.3. فاصل مغلق
وهي تختلف عن الفجوة المفتوحة بنقطتين فقط (النهايتين) و . لكن هذا الاختلاف أساسي وهام، كما سنرى لاحقًا، على سبيل المثال، عند دراسة خصائص الدوال.
حذف عبارة "مجموعة جميع الأرقام (النقاط)" سمثل ذلك"، وما إلى ذلك، نلاحظ كذلك:
و 
، يعني 
و 
فترات نصف مفتوحة أو نصف مغلقة (أحيانًا: نصف فترات)؛
أو 
وسائل: 
أو 
ويتم تعيينه 
أو 
;
أو 
وسائل 
أو 
ويتم تعيينه 
أو 
;
، يعني 
مجموعة جميع الأعداد الحقيقية شارات 
رموز "اللانهاية"؛ يطلق عليهم أرقام غير صحيحة أو مثالية. 
§1.3. القيمة المطلقة (أو المعامل) لعدد حقيقي
تعريف. القيمة المطلقة (أو الوحدة)الرقم يسمى الرقم نفسه إذا 
أو 
لو 
. يشار إلى القيمة المطلقة بالرمز 
. لذا، 
على سبيل المثال، 
, 
, 
.
هندسيا يعني مسافة النقطة أإلى الأصل. إذا كان لدينا نقطتين و، فيمكن تمثيل المسافة بينهما على النحو التالي 
(أو 
). على سبيل المثال، 
ثم المسافة 
.
خواص الكميات المطلقة.
1. من التعريف يتبع ذلك 
, 
، إنه 
.
2. القيمة المطلقة للمجموع والفرق لا تتجاوز مجموع القيم المطلقة: 
.
1) إذا 
، الذي - التي 
. 2) إذا 
، الذي - التي . ▲
3. 
.
، ثم حسب الخاصية 2: 
، أي. 
. وكذلك لو تخيلت 
، ثم نصل إلى عدم المساواة 
▲
4. 
- يتبع من التعريف: النظر في الحالات 
و 
.
5. 
، بشرط 
ويترتب على ذلك من التعريف.
6. عدم المساواة 
,
، وسائل 
. يتم تلبية هذا التباين بالنقاط التي تقع بينهما 
و 
.
7. عدم المساواة 
يعادل عدم المساواة 
، أي. . هذه هي الفترة التي تتمحور حول نقطة الطول 
. تسمى 
جوار نقطة (رقم). لو 
، فيسمى الحي مثقوبًا: هذا أو 
. (الشكل 1.4).
8. 
ومن هنا يترتب على ذلك عدم المساواة 
(
) يعادل عدم المساواة 
أو 
; وعدم المساواة 
يحدد مجموعة من النقاط التي 
، أي. هذه نقاط تقع خارج القطعة 
، بالضبط: 
و 
.
§1.4. بعض المفاهيم والملاحظات
دعونا نقدم بعض المفاهيم والرموز المستخدمة على نطاق واسع من نظرية المجموعات والمنطق الرياضي وفروع أخرى من الرياضيات الحديثة.
1 . مفهوم مجموعاتهي واحدة من الأساسيات في الرياضيات، أولية، عالمية - وبالتالي لا يمكن تعريفها. لا يمكن وصفها (استبدالها بالمرادفات) إلا: إنها مجموعة، مجموعة من بعض الأشياء، الأشياء، متحدة ببعض الخصائص. تسمى هذه الكائنات عناصرالجموع. أمثلة: العديد من حبات الرمل على الشاطئ، النجوم في الكون، الطلاب في الفصل الدراسي، جذور المعادلة، نقاط القطعة. يتم استدعاء المجموعات التي عناصرها أرقام مجموعات رقمية. بالنسبة لبعض المجموعات القياسية، يتم تقديم تدوين خاص، على سبيل المثال، ن,ز,ص-انظر الفقرة 1.1.
يترك أ- كثير و سهو عنصرها، ثم يكتبون: 
; يقرأ " سينتمي أ» ( 
علامة التضمين للعناصر). إذا كان الكائن سغير مدرجة في أ، ثم يكتبون 
; يقرأ: " سلا ينتمي أ" على سبيل المثال، 
ن; 8,51
ن; لكن 8.51 
ر.
لو سهو تسمية عامة لعناصر المجموعة أ، ثم يكتبون 
. إذا كان من الممكن كتابة تسمية جميع العناصر، فاكتب 
, 
الخ. المجموعة التي لا تحتوي على عنصر واحد تسمى مجموعة فارغة ويرمز لها بالرمز ؛ على سبيل المثال، مجموعة الجذور (الحقيقية) للمعادلة 
هناك فارغة.
المجموعة تسمى أخيرإذا كانت مكونة من عدد محدود من العناصر. إذا، بغض النظر عن العدد الطبيعي N، في المجموعة أهناك عناصر أكثر من N، إذن أمُسَمًّى بلا نهايةمجموعة: هناك عدد لا نهائي من العناصر فيه.
إذا كان كل عنصر من عناصر المجموعة ^ أينتمي للكثيرين ب، الذي - التي 
يسمى جزء أو مجموعة فرعية من مجموعة بوالكتابة 
; يقرأ " أالواردة في ب» ( 
هناك علامة إدراج للمجموعات). على سبيل المثال، نزر.لو 
، ثم يقولون أن المجموعات أو بمتساوون والكتابة 
. وإلا يكتبون 
. على سبيل المثال، إذا 
، أ 
مجموعة جذور المعادلة 
، الذي - التي .
مجموعة عناصر كلا المجموعتين أو بمُسَمًّى توحيدمجموعات ويشار إليها 
(أحيانا 
). مجموعة من العناصر التي تنتمي إلى و أو ب، مُسَمًّى تداخلمجموعات ويشار إليها 
. مجموعة جميع عناصر المجموعة ^ أ، والتي لم ترد في ب، مُسَمًّى اختلافمجموعات ويشار إليها 
. ويمكن تمثيل هذه العمليات تخطيطيا على النحو التالي:
إذا أمكن إنشاء تطابق واحد لواحد بين عناصر المجموعات، فإنهم يقولون أن هذه المجموعات متكافئة ويكتبون 
. أي مجموعة أ، أي ما يعادل مجموعة الأعداد الطبيعية ن= دعا معدودةأو معدودة.بمعنى آخر، تسمى المجموعة قابلة للعد إذا كان من الممكن ترقيم عناصرها وترتيبها في عدد لا نهائي التبعية 
، وجميع أعضائها مختلفون: 
في 
، ويمكن كتابتها على الشكل . يتم استدعاء مجموعات أخرى لا حصر لها لا يحصى. قابلة للعد، باستثناء المجموعة نفسها ن،سيكون هناك، على سبيل المثال، مجموعات 
, ز.اتضح أن مجموعات جميع الأعداد العقلانية والجبرية قابلة للعد، والمجموعات المكافئة لجميع الأعداد غير المنطقية والمتسامية والحقيقية والنقاط لأي فترة غير قابلة للعد. يقولون أن الأخير لديه قوة الاستمرارية (القوة هي تعميم لمفهوم عدد (عدد) العناصر لمجموعة لا نهائية).
2
. يجب أن يكون هناك بيانان، حقيقتان: و 
. رمز 
تعني: "إذا كان صحيحًا، فهو صحيح و" أو "يتبع"، "يعني أن جذر المعادلة له خاصية من اللغة الإنجليزية يخرج- يخرج.
دخول: 
، أو 
يعني: هناك كائن (واحد على الأقل) له الخاصية 
. والتسجيل 
، أو 
، يعني: كل شخص له الملك. وعلى وجه الخصوص يمكننا أن نكتب: 
و .
ويمكن الحصول على تمثيل هندسي معبر لنظام الأعداد النسبية على النحو التالي.
على خط مستقيم معين، "المحور العددي"، نحدد المقطع من O إلى 1 (الشكل 8). يحدد هذا طول مقطع الوحدة، والذي، بشكل عام، يمكن اختياره بشكل تعسفي. يتم بعد ذلك تمثيل الأعداد الصحيحة الموجبة والسالبة بمجموعة من النقاط المتباعدة بشكل متساوٍ على محور العدد، أي يتم وضع علامة على الأرقام الموجبة على اليمين، والأرقام السالبة على يسار النقطة 0. لتصوير الأرقام ذات المقام n، نقسم كلًا من الأعداد الصحيحة الموجبة والسالبة على يسار النقطة 0. الأجزاء الناتجة من طول الوحدة إلى n أجزاء متساوية؛ ستمثل نقاط القسمة الكسور ذات المقام n. إذا فعلنا ذلك بالنسبة لقيم n المقابلة لجميع الأعداد الطبيعية، فسيتم تصوير كل رقم نسبي بنقطة ما على محور العدد. سوف نتفق على تسمية هذه النقاط بـ”العقلانية”. بشكل عام، سوف نستخدم مصطلحي "الرقم النسبي" و"النقطة النسبية" كمرادفين.
في الفصل الأول، الفقرة 1، تم تعريف علاقة المتباينة A لأي زوج من النقاط النسبية، فمن الطبيعي محاولة تعميم علاقة المتباينة الحسابية بطريقة تحافظ على هذا الترتيب الهندسي للنقاط قيد النظر. وهذا ممكن إذا قبلنا التعريف التالي: يقولون أن العدد النسبي A أقلمن الرقم العقلاني B (A أكبر من الرقم A (B>A)، إذا الفرق فاإيجابي. وهذا يعني (لأ بين A وB هي تلك التي تكون >A وقطعة (أو شريحة) ويشار إليه بـ [A، B] (ومجموعة النقاط الوسيطة وحدها هي فاصلة(أو ما بين أثنين) ، يُشار إليه بـ (أ، ب)).
تسمى مسافة النقطة الاختيارية A من الأصل 0، والتي تعتبر رقمًا موجبًا قيمه مطلقه A ويشار إليه بالرمز
يتم تعريف مفهوم "القيمة المطلقة" على النحو التالي: إذا كانت A≥0، ثم |A| = أ؛ اذا كان
|أ + ب|≥|أ| + |ب|،
وهذا صحيح بغض النظر عن إشارات A وB.
يتم التعبير عن حقيقة ذات أهمية أساسية من خلال الجملة التالية: النقاط العقلانية موجودة بكثافة في كل مكان على خط الأعداد. ومعنى هذه العبارة أن كل فترة، مهما كانت صغيرة، تحتوي على نقاط منطقية. للتحقق من صحة العبارة المذكورة، يكفي أن نأخذ الرقم n كبيرًا جدًا بحيث يكون الفاصل الزمني أقل من الفاصل الزمني المحدد (A، B)؛ عندها ستكون إحدى نقاط العرض على الأقل داخل هذه الفترة. لذا، لا يوجد مثل هذا الفاصل الزمني على خط الأعداد (حتى أصغر فترة يمكن تخيلها) لا توجد ضمنها نقاط منطقية. وهذا يؤدي إلى نتيجة طبيعية أخرى: كل فترة تحتوي على مجموعة لا حصر لها من النقاط المنطقية. بل لو كانت فترة معينة لا تحتوي إلا على عدد منتهٍ من النقاط المنطقية، فإنه في الفترة التي تكونها نقطتان متجاورتان من هذه النقطتين لم يعد هناك نقاط منطقية، وهذا يخالف ما ثبت.
التذكرة 1
عاقِلالأرقام - الأرقام المكتوبة بالشكل p/q، حيث q عدد طبيعي. رقم، وp هو عدد صحيح.
الرقمان a=p1/q1 و b=p2/q2 متساويان إذا كان p1q2=p2q1، و p2q1 و a>b إذا كانت p1q2
التذكرة 2
ارقام مركبة.ارقام مركبة
المعادلة الجبرية هي معادلة من الشكل: P n ( س) = 0، حيث P n ( س) - متعدد الحدود ن- يا درجة. زوجان من الأعداد الحقيقية سو فيدعنا نسميها مرتبة إذا تمت الإشارة إلى أي منهما يعتبر أولاً وأيهما يعتبر ثانيًا. تدوين الزوج المرتب: ( س, ذ). العدد المركب هو زوج مرتب عشوائيًا من الأعداد الحقيقية. ض = (س, ذ)-عدد مركب.
س-الجزء الحقيقي ض, ذ-الجزء الخيالي ض. لو س= 0 و ذ= 0 إذن ض= 0. خذ بعين الاعتبار z 1 = (x 1 , y 1) و z 2 = (x 2 , y 2).
التعريف 1.ض 1 = ض 2 إذا كان س 1 = س 2 و ص 1 = ص 2.
مفاهيم > و< для комплексных чисел не вводятся.
التمثيل الهندسي والشكل المثلثي للأعداد المركبة.
م( س, ذ) « ض = س + iy.
½ أوم½ = ص =½ ض½ = .(صورة)
r يسمى معامل العدد المركب ض.
j يسمى وسيطة الرقم المركب ض. يتم تحديده بدقة ± 2p ن.
X= آركوسج، ذ= رسينج.
ض= س+ iy= ص (كوسج + أنا Sinj) هو الشكل المثلثي للأعداد المركبة.
البيان 3.
= (كوس + أناالخطيئة)،
= (كوس + أناالذنب) ثم
= (كوس (+) + أناالخطيئة ( + ))،
= (كوس (-)+ أناالخطيئة ( - )) عند ¹0.
البيان 4.
لو ض=r(cosj+ أناسينج)، ثم "طبيعي ن:
= (كوس نج + أناخطيئة نيوجيرسي),
التذكرة 3
يترك X- مجموعة رقمية تحتوي على رقم واحد على الأقل (مجموعة غير فارغة).
سÎ X- سالواردة في X. ; سÏ X- سلا ينتمي X.
تعريف: مجموعة من Xويسمى يحدها أعلاه (أدناه) إذا كان هناك رقم م(م) بحيث لأي س Î Xعدم المساواة يحمل س £ م (س ³ م)، بينما الرقم ميسمى الحد العلوي (السفلي) للمجموعة X. مجموعة من Xويقال أن يحدها أعلاه إذا $ م, " س Î X: س £ م. تعريفمجموعة غير محدودة من فوق. مجموعة من Xيقال أنه غير محدود من فوق إذا " م $ س Î X: س> م. التعريفمجموعة من Xيسمى محددًا إذا كان محددًا من الأعلى والأسفل، أي $ م, ممثل ذلك " س Î X: م £ س £ م.تعريف مكافئ للغول mn-va: Set Xيسمى يحدها إذا $ أ > 0, " س Î X: ½ س½£ أ. التعريف: أصغر حد أعلى لمجموعة محدودة من الأعلى Xويسمى لها العليا، ويشار إليه سوب X
(الأعلى). = سوب X. وبالمثل، يمكن للمرء أن يحدد بالضبط
الحافة السفلية. مقابل تعريفالحد الأعلى الدقيق:
الرقم يسمى أعلى المجموعة X، لو: 1) " س Î X: X£ (يوضح هذا الشرط أنه أحد الحدود العليا). 2) " < $ x Î X: X> (هذا الشرط يوضح أن -
أصغر الوجوه العلوية).
رشفة X= :
1. " سÎ X: س £ .
2. " < $ سÎ X: س> .
الوقود النووي المشع X(الناقص) هو الناقص بالضبط. دعونا نطرح السؤال: هل كل مجموعة محدودة لها حواف محددة؟
مثال: X= {س: س>0) ليس لديه رقم أصغر.
نظرية وجود وجه علوي (سفلي) دقيق. أي حد علوي (سفلي) غير فارغ xÎR له وجه علوي (سفلي) محدد.
نظرية قابلية فصل الأعداد العددية:▀▀▄
التذكرة 4
إذا تم تخصيص رقم مقابل لكل عدد طبيعي n (n=1,2,3..) Xn، فيقولون إنه محدد ومعطى التبعية x1, x2..., اكتب (Xn), (Xn) مثال: Xn=(-1)^n: -1,1,-1,1,... اسم النهاية. من الأعلى (من الأسفل) إذا كانت مجموعة النقاط x=x1,x2,…xn الواقعة على المحور العددي محدودة من الأعلى (من الأسفل)، أي. $C:Xn$C" حد التسلسل:يُطلق على الرقم a حد التسلسل إذا كان لأي ε>0 $ : N (N=N/(ε)). "n>N عدم المساواة |Xn-a|<ε. Т.е. – ε
في ن>ن.
تفرد الحدتسلسل محدود ومتقارب
الخاصية 1: التسلسل المتقارب له نهاية واحدة فقط.
الدليل : بالتناقض دع أو بحدود التسلسل المتقارب (x n)، وa لا يساوي b. النظر في تسلسلات متناهية الصغر (α n )=(x n -a) و (β n )=(x n -b). لأن جميع العناصر ب.م. التسلسلات (α n -β n ) لها نفس القيمة b-a، ثم بواسطة خاصية b.m. تسلسلات ب-أ=0 أي b=a وقد وصلنا إلى التناقض.
الخاصية 2: يحدها تسلسل متقارب.
البرهان: لتكن a نهاية المتتابعة المتقاربة (x n)، فإن α n = x n -a عنصر من عناصر b.m. تسلسلات. لنأخذ أي ε>0 ونستخدمه للعثور على N ε: / x n -a/< ε при n>ن ε . دعونا نشير بـ b إلى أكبر الأرقام ε+/а/, /x1/, /x2/,…,/x N ε-1 /,x N ε. ومن الواضح أن / س ن /
ملاحظة: قد لا يكون التسلسل المحدد متقاربًا.
التذكرة 6
ويسمى التسلسل a n متناهية الصغر، مما يعني أن نهاية هذا التسلسل بعده هو 0.
a n – متناهية الصغر Û lim(n ® + ¥)a n =0 أي أنه لأي ε>0 يوجد N بحيث لأي n>N |a n |<ε
نظرية.مجموع متناهية الصغر هو متناهية الصغر.
أ ن ب ن ® متناهية الصغر Þ أ ن + ب ن – متناهية الصغر.
دليل.
a n - متناهية الصغر Û "ε>0 $ N 1:" n >N 1 Þ |a n |<ε
b n - متناهية الصغر Û "ε>0 $ N 2:" n >N 2 Þ |b n |<ε
دعونا نحدد N=max(N 1 ,N 2 )، ثم لأي n>N Þ يتم تحقيق كلا المتباينتين في نفس الوقت:
|أ ن |<ε |a n +b n |£|a n |+|b n |<ε+ε=2ε=ε 1 "n>ن
دعونا نضبط "ε 1 >0, set ε=ε 1 /2. ثم لأي ε 1 >0 $N=maxN 1 N 2: " n>N Þ |a n +b n |<ε 1 Û lim(n ® ¥)(a n +b n)=0, то
هو ن + ب ن – متناهية الصغر.
نظريةمنتج متناهية الصغر هو متناهية الصغر.
أ ن ,ب ن – متناهية الصغر Þ أ ن ب ن – متناهية الصغر.
شهادة:
لنضع "ε 1 >0، ونضع ε=Öε 1، نظرًا لأن a n وb n متناهية الصغر بالنسبة إلى ε>0، إذن هناك N 1: " n>N Þ |a n |<ε
$N 2: " n>N 2 Þ |b n |<ε
لنأخذ N=max (N 1 ;N 2 )، ثم "n>N = |a n |<ε
|أ ن ب ن |=|أ ن ||ب ن |<ε 2 =ε 1
" ε 1 >0 $N:"n>N |a n b n |<ε 2 =ε 1
lim a n b n =0 Û a n b n – متناهية الصغر، وهو ما يحتاج إلى إثبات.
نظريةمنتج تسلسل محدود وتسلسل متناهي الصغر هو تسلسل متناهي الصغر
و n هو تسلسل محدود
أ ن – تسلسل متناهية الصغر Þ أ ن ن – تسلسل متناهية الصغر.
الدليل: بما أن n محدد بـ Û $С>0: "nО نÞ |أ ن |ج
دعونا نضبط "ε 1 >0; set ε=ε 1 /C; بما أن n متناهية الصغر، إذن ε>0 $N:"n>NÞ |a n |<εÞ |a n a n |=|a n ||a n | "ε 1 >0 $N: "n>N Þ |a n a n |=Cε=ε 1 Þ lim(n ® ¥) a n a n =0Û a n a n – متناهية الصغر يسمى التسلسل بي بي بي(بالتسلسل) إذا كتبوا. ومن الواضح أن BBP ليست محدودة. العبارة المعاكسة خاطئة بشكل عام (مثال). إذا للكبيرة نالأعضاء، ثم كتابة هذا يعني أنه في أقرب وقت. يتم تحديد معنى الإدخال بالمثل تسلسلات كبيرة بلا حدودن = 2 ن ;
ب ن =(-1) ن 2 ن ;ج ن =-2 ن تعريف(تسلسلات كبيرة بلا حدود) 1) lim(n ® ¥)a n =+¥، إذا كان "ε>0$N:"n>N Þ a n >ε حيث ε صغير بشكل تعسفي. 2) lim(n ® ¥)a n =-¥، إذا كان "ε>0 $N:"n>N Þ a n<-ε 3) lim(n ® ¥)a n =¥ Û "ε>0 $N:"n>N Þ |a n |>ε التذكرة 7 نظرية "في التقارب الرتيب. آخر" أي تسلسل رتيب متقارب، أي. له حدود. وثيقةدع التسلسل (xn) يتزايد بشكل رتيب. ومحدود من فوق. X - مجموعة الأرقام الكاملة التي تقبل عنصر هذا التسلسل وفقًا للاتفاقية. وبالتالي فإن النظريات محدودة العدد، وفقًا لـ النظرية لها حد أعلى محدد. وجه سوبكس xn®supX (نشير إلى سوبكس بواسطة x*). لأن ×*الأعلى بالضبط. الوجه، ثم xn £x* " n. " e >0 العصب خارج $ xm (دع m يكون n بغطاء): xm>x*-e مع " n>m => من المتباينتين المشار إليهما التي حصلنا عليها المتباينة الثانية x*-e £xn £ x*+e لـ n>m تعادل ½xn-x*1 التذكرة 8 الأس أو الرقم ه R-الرقم الروماني تسلسل بمصطلح مشترك xn=(1+1/n)^n (للأس n)(1) . وتبين أن المتتابعة (1) تزداد رتابة، ومحدودة من الأعلى ومتقاربة، وتسمى نهاية هذه المتتابعة أسية ويرمز لها بالرمز e»2.7128... رقم ه التذكرة 9 مبدأ الأجزاء المتداخلة دع خط الأعداد يُعطى تسلسلاً من الأجزاء ،،...،،... علاوة على ذلك، فإن هذه القطاعات تلبي ما يلي. حالة: 1) كل واحدة لاحقة متداخلة في السابقة، أي. م, "ن=1,2,…; 2) أطوال المقاطع ®0 مع زيادة n، أي. ليم(n®¥)(bn-an)=0. تسمى التسلسلات مع القديسين المحددين متداخلة. نظريةيحتوي أي تسلسل من المقاطع المتداخلة على نقطة واحدة c تنتمي إلى جميع مقاطع التسلسل في وقت واحد، مع النقطة المشتركة لجميع المقاطع التي تم التعاقد عليها. وثيقة(أ) - تسلسل الأطراف اليسرى لأجزاء من الظواهر. رتابة غير متناقصة ويحدها من الأعلى الرقم b1. (bn) - تسلسل النهايات الصحيحة لا يتزايد بشكل رتيب، وبالتالي هذه التسلسلات من الظواهر. متقاربة، أي هناك أرقام c1=lim(n®¥)an وc2=lim(n®¥)bn => c1=c2 => c - هم معنى عام. في الواقع، لها النهاية lim(n®¥)(bn-an)= lim(n®¥)(bn)- lim(n®¥)(an) بسبب الشرط 2) o= lim(n®¥) (bn- an)=с2-с1=> с1=с2=с ومن الواضح أن t.c شائع في جميع القطاعات، حيث أن "n an £ c £ bn. والآن سنثبت أنه واحد. لنفترض أن $ هو c' آخر يتم التعاقد معه على كافة القطاعات. إذا أخذنا أي قطع غير متقاطعة c وc'، فيجب أن يقع "ذيل" التسلسلات (an) و(bn) بالكامل على جانب واحد بالقرب من النقطة c'' (بما أن an و bn يتقاربان ج و ج' في وقت واحد). التناقض صحيح. التذكرة 10 نظرية بولزانو فايرستراس
من أي قطع. بعد ذلك يمكنك اختيار التجمع. مقطع فرعي 1. بما أن التسلسل محدود، إذن $ m وM، بحيث يكون " m £ xn £ M، " n. D1= - المقطع الذي تقع فيه جميع تسلسلات t-ki. دعونا نقسمها إلى نصفين. سيحتوي واحد على الأقل من النصفين على عدد لا نهائي رقم ر كبعد. D2 هو النصف الذي يوجد فيه عدد لا نهائي من تسلسلات t-k. نحن نقسمها إلى نصفين. على الأقل في واحدة من نصفين سلبي. يحتوي D2 على عدد لا نهائي من التسلسلات. هذا النصف هو D3. تقسيم القطعة D3...إلخ. نحصل على سلسلة من المقاطع المتداخلة، أطوالها تميل إلى 0. وفقًا لقاعدة المقاطع المتداخلة، وحدات $. تي كا إس، قطة. الانتماء جميع شرائح D1، أي تي تو Dn1. في القطعة D2 أختار النقطة xn2، بحيث تكون n2>n1. في الجزء د3...إلخ. ونتيجة لذلك، الكلمة الأخيرة هي xnkÎDk. التذكرة 11 التذكرة 12 أساسي وفي الختام نتناول مسألة معيار تقارب المتتابعة العددية. دع أي: حصلنا على البيان التالي: فإذا تقاربت المتتابعة، يكون الشرط قد تحقق كوشي: يسمى التسلسل الرقمي الذي يحقق شرط كوشي أساسي. ويمكن إثبات أن العكس صحيح أيضًا. وبذلك يكون لدينا معيار (الشرط الضروري والكافي) لتقارب المتتابعة. معيار كوشي. لكي يكون للمتتابعة حد، من الضروري والكافي أن تكون أساسية. المعنى الثاني لمعيار كوشي.أعضاء التسلسل وأين نو م– أي يقترب بلا حدود عند . التذكرة 13 حدود من جانب واحد. التعريف 13.11.رقم أيسمى حد الدالة ص = و(س) في X، نسعى جاهدين لإجل × 0اليسار (اليمين)، إذا كان هذا | و(خ)-أ|<ε при س 0 - س< δ
(س - س 0< δ
). التسميات: النظرية 13.1 (التعريف الثاني للحد).وظيفة ص = و (س)لديه في X،نسعى جاهدين لإجل X 0، الحد يساوي أ، إذا وفقط إذا كانت كلا النهايتين من جانب واحد عند هذه النقطة موجودتين ومتساويتين أ. دليل. 1) إذا ، ثم ومن أجل س 0 - س< δ, и для س - س 0< δ
|و(خ) - أ|<ε, то есть 1) إذا كان هناك δ 1: | و(خ) - أ| < ε при س 0 - س< δ 1 и δ 2: |و(خ) - أ| < ε при س - س 0<
δ2. باختيار الرقم الأصغر من الأرقام δ 1 و δ 2 وأخذه على أنه δ، نحصل على ذلك من أجل | س - س 0| < δ |و(خ) - أ| < ε, то есть . Теорема доказана. تعليق. وبما أنه قد تم إثبات تكافؤ المتطلبات الواردة في تعريف الحد 13.7 وشروط وجود وتساوي النهايات من جانب واحد، فيمكن اعتبار هذا الشرط هو التعريف الثاني للحد. التعريف 4 (حسب هاينه) رقم أيُسمى حد الدالة في حالة تقارب أي قيم BBP للوسيطة، فإن تسلسل قيم الدالة المقابلة يتقارب أ. التعريف 4 (حسب كوشي). رقم أدعا إذا . وقد ثبت أن هذه التعريفات متكافئة. التذكرة 14 و 15 خصائص نهاية الوظيفة عند نقطة ما 1) إذا كان هناك حد فهو الوحيد 2) إذا كان في tka x0 حد الدالة f(x) lim(x®x0)f(x)=A lim(x®x0)g(x)GBB=> ففي هذه الحالة $ هو حد المجموع والفرق والمنتج والحاصل. الفصل بين هاتين الوظيفتين. أ) ليم(x®x0)(f(x)±g(x))=A±B ب) ليم(x®x0)(f(x)*g(x))=A*B ج) ليم(x®x0)(f(x):g(x))=A/B د) ليم(x®x0)C=C ه) ليم(x®x0)C*f(x)=C*A النظرية 3. لو ( احترام أ ) ثم $ الحي الذي يوجد فيه عدم المساواة > ب (الإجابة الافتراض في النظرية 3 ب=0فنحصل على : إذا ( احتراما)، ثم $ ، في جميع النقاط، والتي ستكون > 0 (التعليق<0),
أولئك. الدالة تحافظ على علامة حدها. النظرية 4(عند العبور إلى الحد في عدم المساواة). إذا كان الشرط في بعض المناطق المجاورة لنقطة ما (ربما باستثناء هذه النقطة نفسها) مستوفيًا وكانت لهذه الوظائف حدود عند هذه النقطة، إذن. في اللغة و. دعونا نقدم الوظيفة. ومن الواضح أنه في محيط ر . ومن ثم، وفقًا لنظرية حفظ الدالة، لدينا قيمة حدها، لكن النظرية 5.(على حد وظيفة وسيطة). (١) إذا التذكرة 16 التعريف 14.1.وظيفة ص=α(س) يسمى متناهية الصغر في س → س 0،لو خصائص متناهية الصغر. 1. مجموع اثنين من المتناهيات في الصغر هو متناهي الصغر. دليل. لو α(س) و بيتا(س) - متناهية الصغر في س → س 0، ثم يوجد δ 1 و δ 2 بحيث | α(س)|<ε/2 и |β(س)|<ε/2 для выбранного значения ε. Тогда |α(x)+β(x)|≥|α(x)|+|β(x)|<ε, то есть |(α(س)+β(س))-0|<ε. Следовательно, تعليق. ويترتب على ذلك أن مجموع أي عدد محدود من المتناهيات في الصغر هو متناهي الصغر. 2. إذا α( X) - متناهية الصغر في س → س 0، أ و(س) - دالة محدودة في حي معين × 0، الذي - التي α(س)و(س) - متناهية الصغر في س → س 0. دليل. دعونا نختار رقما مبحيث | و(خ)| النتيجة الطبيعية 1. إن حاصل ضرب العدد المتناهي في الصغر بعدد محدود هو عدد متناهي الصغر. النتيجة الطبيعية 2. منتج اثنين أو أكثر من متناهية الصغر هو متناهية الصغر. النتيجة الطبيعية 3. المجموعة الخطية من متناهية الصغر هي متناهية الصغر. 3. (التعريف الثالث للحد). إذا، فالشرط الضروري والكافي لذلك هو تلك الوظيفة و(س) يمكن تمثيلها في النموذج و(س)=أ+α(س)، أين α(س) - متناهية الصغر في س → س 0. دليل. 1)
دع ثم | و(خ)-أ|<ε при س → س 0، إنه α(x)=f(x)-A- متناهية الصغر في س → س 0 .لذلك ، و(س)=أ+α(س). 2) دع و(س)=أ+α(س). ثم تعليق. وبذلك يتم الحصول على تعريف آخر للحد يعادل التعريفين السابقين. وظائف كبيرة بلا حدود. التعريف 15.1. يقال إن الدالة f(x) كبيرة بلا حدود لـ x x 0 if بالنسبة للكبيرة بلا حدود، يمكنك تقديم نفس نظام التصنيف كما هو الحال بالنسبة للصغير بلا حدود، وهي: 1. تعتبر f(x) وg(x) كبيرة بلا حدود كميات من نفس الترتيب إذا 2. إذا كانت f(x) تعتبر كبيرة بلا حدود وبرتبة أعلى من g(x). 3. يُطلق على f(x) الكبير بشكل لا نهائي كمية من الرتبة k نسبة إلى g(x) كبير بشكل لا نهائي إذا . تعليق. لاحظ أن x كبير بشكل لا نهائي (لـ a> 1 و x) بترتيب أعلى من x k لأي k، وlog a x كبير بشكل لا نهائي بترتيب أقل من أي قوة x k. نظرية 15.1. إذا كانت α(x) صغيرة بلا حدود مثل x→x 0، فإن 1/α(x) كبيرة بلا حدود مثل x→x 0. دليل. دعونا نثبت ذلك من أجل |x - x 0 |< δ. Для этого достаточно выбрать в качестве ε 1/M. Тогда при |x - x 0 | < δ |α(x)|<1/M, следовательно, |1/α(x)|>م. وهذا يعني أن 1/α(x) كبير بشكل لا نهائي مثل x→x 0. التذكرة 17 النظرية 14.7 (الحد الأول الملحوظ). . دليل. خذ بعين الاعتبار دائرة نصف قطرها وحدة ومركزها نقطة الأصل وافترض أن الزاوية AOB تساوي x (راديان). دعونا نقارن مساحات المثلث AOB والقطاع AOB والمثلث AOC، حيث يكون نظام التشغيل للخط المستقيم مماسًا للدائرة التي تمر عبر النقطة (1؛0). من الواضح أن . باستخدام الصيغ الهندسية المقابلة لمساحات الأشكال، نحصل على ذلك الأعداد الحقيقية II § 44 التمثيل الهندسي للأعداد الحقيقية الأعداد الحقيقية هندسيًا، مثل الأعداد النسبية، يتم تمثيلها بنقاط على الخط. يترك ل
هو خط مستقيم اعتباطي، وO هي بعض نقاطه (شكل 58). كل عدد حقيقي موجب α
دعونا نربط النقطة A، التي تقع على يمين O على مسافة α
وحدات الطول. إذا، على سبيل المثال، α
= 2.1356... إذن 2 < α
< 3 إلخ. ومن الواضح أن النقطة (أ) في هذه الحالة يجب أن تكون على الخط المستقيم ل
على يمين النقاط المقابلة للأرقام 2; 2,1; 2,13; ... , ولكن على يسار النقاط المقابلة للأرقام 3; 2,2; 2,14; ... . ويمكن إثبات أن هذه الشروط تحدد على الخط ل
النقطة الوحيدة A التي نعتبرها صورة هندسية لعدد حقيقي α
= 2,1356... . وبالمثل، لكل عدد حقيقي سلبي β
دعونا نربط النقطة B التي تقع على يسار O على مسافة | β |
وحدات الطول. وأخيرًا، نربط الرقم "صفر" بالنقطة O. لذلك، سيتم تصوير الرقم 1 على خط مستقيم ل
النقطة A، الواقعة على يمين O على مسافة وحدة طول واحدة (الشكل 59)، الرقم - √2 - بالنقطة B، الواقعة على يسار O على مسافة √2 وحدة طول، إلخ . دعونا نظهر كيف على خط مستقيم ل
باستخدام البوصلة والمسطرة، يمكنك العثور على نقاط تتوافق مع الأعداد الحقيقية √2، √3، √4، √5، إلخ. وللقيام بذلك، سنوضح أولاً كيف يمكنك إنشاء مقاطع يتم التعبير عن أطوالها بهذه الأرقام. لتكن AB قطعة مأخوذة كوحدة طول (الشكل 60). عند النقطة A، نبني عمودًا على هذا الجزء ونرسم عليه القطعة AC مساوية للقطعة AB. وبعد ذلك، بتطبيق نظرية فيثاغورس على المثلث القائم ABC، نحصل على: BC = √AB 2 + AC 2 = √1+1 = √2 ولذلك، فإن طول القطعة BC هو √2. الآن لنقم بإنشاء خط عمودي على القطعة BC عند النقطة C ونحدد النقطة D عليها بحيث تكون القطعة CD مساوية لوحدة واحدة من الطول AB. ثم من المثلث القائم BCD نجد: ВD = √ВC 2 + СD 2 = √2+1 = √3 ولذلك، فإن طول القطعة BD هو √3. بمواصلة العملية الموضحة أكثر، يمكننا الحصول على المقاطع BE، BF، ...، والتي يتم التعبير عن أطوالها بالأرقام √4، √5، إلخ. الآن على خط مستقيم ل
من السهل العثور على تلك النقاط التي تمثل تمثيلًا هندسيًا للأعداد √2، √3، √4، √5، إلخ. من خلال وضع، على سبيل المثال، القطعة BC على يمين النقطة O (الشكل 61)، نحصل على النقطة C، التي تعمل كصورة هندسية للرقم √2. وبنفس الطريقة، بوضع القطعة BD على يمين النقطة O، نحصل على النقطة D"، وهي الصورة الهندسية للرقم √3، إلخ. ومع ذلك، لا ينبغي لأحد أن يفكر في استخدام البوصلة والمسطرة على خط الأعداد ل
يمكن للمرء العثور على النقطة المقابلة لأي رقم حقيقي معين. لقد ثبت، على سبيل المثال، أنه مع وجود بوصلة ومسطرة فقط تحت تصرفك، فمن المستحيل إنشاء قطعة يتم التعبير عن طولها بالرقم π
= 3.14... . لذلك، على خط الأعداد ل
وبمساعدة مثل هذه الإنشاءات، من المستحيل الإشارة إلى النقطة المقابلة لهذا الرقم، ومع ذلك فإن مثل هذه النقطة موجودة. إذن، لكل عدد حقيقي α
من الممكن ربط نقطة محددة جيدًا بخط مستقيم ل
. وستكون هذه النقطة على مسافة | α
| وحدات الطول وتكون على يمين O if α
> 0، وعلى يسار O، إذا α
< 0. Очевидно, что при этом двум неравным действительным числам будут соответствовать две различные точки прямой ل
. في الواقع، اسمحوا الرقم α
النقطة A يتوافق، والرقم β
- النقطة ب. ثم إذا α
> β
، سيكون A على يمين B (الشكل 62، أ)؛ لو α
< β
، فإن A سوف يقع على يسار B (الشكل 62، ب). في حديثنا في الفقرة 37 عن الصورة الهندسية للأعداد النسبية، طرحنا السؤال: هل يمكن اعتبار أي نقطة على الخط صورة هندسية لبعضها؟ عاقِلأعداد؟ لم نتمكن من الإجابة على هذا السؤال حينها؛ الآن يمكننا الإجابة عليه بكل تأكيد. هناك نقاط على الخط تعمل بمثابة تمثيل هندسي للأعداد غير النسبية (على سبيل المثال، √2). لذلك، ليست كل نقطة على الخط تمثل عددًا نسبيًا. لكن في هذه الحالة يطرح سؤال آخر: هل يمكن اعتبار أي نقطة على خط الأعداد صورة هندسية للبعض؟ صالحأعداد؟ لقد تم بالفعل حل هذه المشكلة بشكل إيجابي. في الواقع، دع A تكون نقطة اعتباطية على الخط ل
، ملقاة على يمين O (الشكل 63). يتم التعبير عن طول المقطع OA بعدد حقيقي موجب α
(انظر الفقرة 41). وبالتالي فإن النقطة A هي صورة هندسية للرقم α
. ومن الثابت بالمثل أن كل نقطة B تقع على يسار O يمكن اعتبارها صورة هندسية لعدد حقيقي سالب - β
، أين β
- طول المقطع VO. وأخيرًا، النقطة O بمثابة تمثيل هندسي للرقم صفر. ومن الواضح أن نقطتين مختلفتين على الخط ل
لا يمكن أن تكون صورة هندسية لنفس العدد الحقيقي. للأسباب المذكورة أعلاه، يسمى الخط المستقيم الذي يشار إليه بنقطة معينة O كنقطة "الابتدائية" (لوحدة طول معينة) رقم الخط. خاتمة. مجموعة كل الأعداد الحقيقية ومجموعة كل النقاط على خط الأعداد متناظرة واحد لواحد. هذا يعني أن كل رقم حقيقي يتوافق مع نقطة واحدة محددة جيدًا على خط الأعداد، وعلى العكس من ذلك، لكل نقطة على خط الأعداد، مع مثل هذه المراسلات، هناك رقم حقيقي واحد محدد جيدًا. تمارين
320. اكتشف أي من النقطتين تقع على اليسار وأيهما على اليمين على خط الأعداد، إذا كانت هذه النقاط تتوافق مع الأرقام: أ) 1.454545... و1.455454...؛ ج) 0 و - 1.56673...؛ ب) - 12.0003... و - 12.0002...؛ د) 13.24...و 13.00.... 321. اكتشف أي من النقطتين تقع على خط الأعداد بعيدًا عن نقطة البداية O، إذا كانت هذه النقاط تتوافق مع الأرقام: أ) 5.2397... و4.4996...؛ .. ج) -0.3567... و 0.3557... . د) - 15.0001 و - 15.1000...؛ 322. في هذا القسم تبين أنه لبناء قطعة من الطول √ ن
باستخدام البوصلة والمسطرة، يمكنك المتابعة على النحو التالي: قم أولاً ببناء قطعة بطول √2، ثم قطعة بطول √3، وما إلى ذلك، حتى نصل إلى قطعة بطول √ ن
. ولكن لكل ثابت ص
> 3 يمكن تسريع هذه العملية. كيف، على سبيل المثال، يمكنك البدء في إنشاء قطعة طولها √10؟ 323*. كيفية استخدام البوصلة والمسطرة للعثور على النقطة على خط الأعداد المقابلة للرقم 1 / α
، إذا كان موضع النقطة مطابقًا للرقم α
، هل هو معروف؟ ارقام مركبة مفاهيم أساسية تعود البيانات الأولية للرقم إلى العصر الحجري - العصر الحجري القديم. وهي "واحد" و"قليل" و"كثير". تم تسجيلها على شكل شقوق وعقد وما إلى ذلك. إن تطور عمليات العمل وظهور الملكية أجبر الإنسان على اختراع الأرقام وأسمائها. ظهرت الأعداد الطبيعية أولاً ن، تم الحصول عليها عن طريق عد الأشياء. ثم، إلى جانب الحاجة إلى العد، كان لدى الناس حاجة إلى قياس الأطوال والمساحات والأحجام والوقت والكميات الأخرى، حيث كان عليهم أن يأخذوا في الاعتبار أجزاء من المقياس المستخدم. هذه هي الطريقة التي ظهرت بها الكسور. تم الإثبات الرسمي لمفاهيم الأعداد الكسرية والسالبة في القرن التاسع عشر. مجموعة من الأعداد الصحيحة ز– هذه هي الأعداد الطبيعية، الأعداد الطبيعية مع علامة الطرح والصفر. تشكل الأعداد الصحيحة والكسرية مجموعة من الأعداد النسبية س،ولكن تبين أيضًا أنها غير كافية لدراسة المتغيرات المتغيرة باستمرار. أظهر سفر التكوين مرة أخرى النقص في الرياضيات: استحالة حل معادلة النموذج X 2 = 3، ولهذا ظهرت الأعداد غير النسبية أنا.اتحاد مجموعة الأعداد العقلانية سوالأرقام غير المنطقية أنا- مجموعة من الأرقام الحقيقية (أو الحقيقية). ر. ونتيجة لذلك، امتلأ خط الأعداد: كل رقم حقيقي يتوافق مع نقطة عليه. ولكن على الكثير رلا توجد طريقة لحل معادلة النموذج X 2 = – أ 2. ومن هنا ظهرت الحاجة مرة أخرى إلى التوسع في مفهوم العدد. هكذا ظهرت الأعداد المركبة عام 1545. وصفها منشئها جيه كاردانو بأنها "سلبية تمامًا". تم تقديم اسم "وهمي" في عام 1637 من قبل الفرنسي ر. ديكارت، وفي عام 1777 اقترح أويلر استخدام الحرف الأول من الرقم الفرنسي أناللدلالة على الوحدة التخيلية. دخل هذا الرمز حيز الاستخدام العام بفضل K. Gauss. خلال القرنين السابع عشر والثامن عشر، استمرت مناقشة الطبيعة الحسابية للتخيلات وتفسيرها الهندسي. اقترح كل من الدنماركي ج. فيسيل، والفرنسي ج. أرغان، والألماني ك. غاوس، بشكل مستقل، تمثيل عدد مركب كنقطة على المستوى الإحداثي. في وقت لاحق اتضح أنه أكثر ملاءمة لتمثيل الرقم ليس بالنقطة نفسها، ولكن بواسطة ناقل يذهب إلى هذه النقطة من الأصل. فقط في نهاية القرن الثامن عشر وبداية القرن التاسع عشر، أخذت الأعداد المركبة مكانها الصحيح في التحليل الرياضي. أول استخدام لها كان في نظرية المعادلات التفاضلية وفي نظرية الديناميكا المائية. التعريف 1.عدد مركبويسمى تعبيرا عن النموذج حيث سو ذهي أعداد حقيقية، و أنا– الوحدة التخيلية . رقمين معقدين و متساويإذا وفقط إذا ، . إذا، فسيتم استدعاء الرقم خيالية بحتة; إذا كان الرقم عددا حقيقيا، فهذا يعني أن المجموعة ر مع، أين مع– مجموعة من الأعداد المركبة . المترافقةإلى عدد مركب يسمى عددا مركبا. التمثيل الهندسي للأعداد المركبة. يمكن تمثيل أي عدد مركب بنقطة م(س, ذ) طائرة أوكسي.يشير زوج من الأعداد الحقيقية أيضًا إلى إحداثيات متجه نصف القطر التعريف 2.الجزء الحقيقي X. تعيين: س= إعادة ض(من اللاتينية رياليس). تعيين: ذ= ايم ض(من اللاتينية إيماجيناريوس). يكرر ضيتم إيداعه على المحور ( أوه)، أنا ضيتم إيداعه على المحور ( أوه)، فإن المتجه المقابل للعدد المركب هو متجه نصف القطر للنقطة م(س, ذ)، (أو م(يكرر ض، أنا ض)) (رسم بياني 1). التعريف 4.يسمى المستوى الذي ترتبط نقاطه بمجموعة من الأعداد المركبة طائرة معقدة. يسمى محور الإحداثي المحور الحقيقيلأنه يحتوي على أرقام حقيقية. يسمى المحور الإحداثي محور وهمي، فهو يحتوي على أرقام مركبة خيالية بحتة. يتم الإشارة إلى مجموعة الأعداد المركبة مع. التعريف 5.وحدةعدد مركب ض = (س, ذ) يسمى طول المتجه:، أي. التعريف 6.دعوىالعدد المركب هو الزاوية المحصورة بين الاتجاه الموجب للمحور ( أوه) والمتجه: 
بالإضافة إلى عدد طبيعي، يمكنك التعويض برقم طبيعي آخر في المتباينة الأخيرة 
،ثم
وفي بعض جوار النقطة (ربما باستثناء النقطة نفسها) يتم استيفاء الشرط (2)، فإن الدالة لها نهاية في النقطة وهذا الحد يساوي أ.بالشرط (1) $ لـ (هنا أصغر حي للنقطة). ولكن بعد ذلك، وبسبب الشرط (2)، ستكون القيمة أيضًا موجودة بالقرب من النقطة أ،أولئك. .
، إنه α(س)+β(س) - متناهي الصغر.
يعني | و(خ)-أ|<ε при |س - س 0| < δ(ε). Cледовательно, .
أو سينكس
2,1 < α
< 2,2
2,13 < α
< 2,14
، أي. بين مجموعة المتجهات على المستوى ومجموعة الأعداد المركبة، يمكن إنشاء تطابق واحد لواحد: .
التعريف 3.الجزء الخياليالعدد المركب هو عدد حقيقي ذ.
.
.
تحميل...
